递归 动态规划

常见递归问题

"算法总结"

Posted by ming on July 25, 2019

“Spring breeze miles, less than to meet you; Clear blue skies, not as good as you are in my heart.”

1. 字符串的全排列/全组合问题

1.1 字符串的全排列

题目描述

输入一个字符串，打印出该字符串中字符的所有排列。例如输入字符abc，则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。

1. 回溯法

递归求全排列，其思想为回溯法。其思路是将一个字符串看成两部分组成：第一部分为第一个字符，第二部分为后面的所有字符。求整个字符串的排列，可以看出两步：首先求所有可能出现在第一个位置的字符，即把第一个字符和后面的所有字符交换；然后固定第一个字符，求后面所有字符的排列。此时仍把后面的字符看成两部分，第一个和后面的字符，然后重复上述步骤(递归).

递归思路

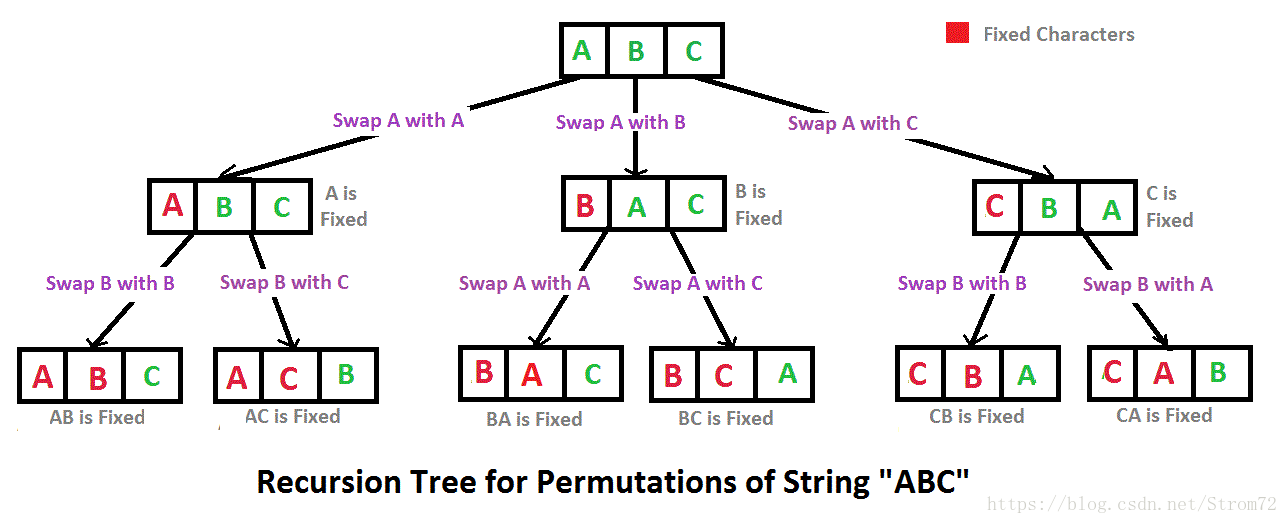
例如上面的这个图，我们的想法是每次都把一个数固定在前面，让后面的数递归地进行全排列，这样每个数都固定过以后就能找出所有排列。关键的地方在于，我们把每个数固定在前面并让后面的进行全排列完毕以后，要恢复原来的状态，也就需要交换回来。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

    public static ArrayList<String> Permutation(String str){
        ArrayList<String> ans = new ArrayList<>();  //排列的全部结果
        if(str != null || str.length() > 0){
            help(0, str.toCharArray(), ans);
            Collections.sort(ans);
        }
        return ans;
    }

    public static void help(int i, char[] cha, ArrayList<String> ans){
        if( i == cha.length - 1){
            String val = String.valueOf(cha);
            if(!ans.contains(val)){
                ans.add(val);
            }
        }else{
            for(int j = i; j < cha.length; j++){
                if(isSwap(cha,i, j)){
                    swap(i, j, cha); //依次选一个数固定住
                    help(i+1, cha, ans); //让后面的进行全排列
                    swap(i,j,cha); //恢复原来的模样，回溯关键
                }
            }
        }
    }

    private static boolean isSwap(char[] cha, int i , int j){
        for(int k = i; k < j; k++){
            if(cha[k] == cha[j]){
                return false;
            }
        }
        return true;
    }

    public static void swap(int i, int j, char[] cha){
        char temp = cha[i];
        cha[i] = cha[j];
        cha[j] = temp;
    }

2. 递归解法

递归还有一种解法，其原理和解题思路1是相同的，只不过换了一种解决思路。它通过创建一个与字符串等长的boolean数组，来标记该位置对于的字符是否已经选择，若被选择，则标记为true；若未选择，则标记为false.具体实现来看代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

    public static void permute(String str){
        int length = str.length();
        boolean[] used = new boolean[length];
        StringBuffer output = new StringBuffer(length);
        permutation3(str,length,output,used,0);
    }

    public static void permutation3(String str,int length, StringBuffer output, boolean[] used, int position){
        if(position == length){
            System.out.println(output.toString());
            return;
        }
        else{
            for (int i = 0; i < length; i++) {
                // skip already used characters
                if(used[i]){
                    continue;
                }
                //add fixed character to output, and mark it as used
                output.append(str.charAt(i));
                used[i] = true;

                permutation3(str,length,output,used,position+1);
                output.deleteCharAt(output.length()-1);
                used[i] = false;
            }
        }
    }

3. 字典序法

首先，我们来详细地讲解一下字典序法。字典序法通常用来解决这样一个问题：给定其中一种排列，求基于字典序的下一种排列。比如给定一种排列为abc，则基于字典序的下一种排列为acb。(要求下一种排列既要比原排列大，又不能有第三种排列位于他俩之间，即下一种排列为大于原排列的最小排列)。

以输入为358764为例，字典序的步骤：

  1. 从原排列中，从右到左，找到第一个左邻小于右邻的字符，记左邻位置为a.(在示例中，a = 1,list[a] = 5)
  2. 重新从右至左，找到第一个比list[a]大的字符，记为位置b。(示例中，b = 4, list[b] = 6)
  3. 交换a和b两个位置的值(示例变成了368754)
  4. 将a后面的数，由小到大排列(示例变成了364578)

算法结束，输出364578.

注意：

  • 第1步中，如果找不到左邻小于右邻的数，则说明给定的排列已经是全排列的最后一个排列了，则直接返回全排列的第一个排列，即所有排列中最小的排列，形成一个循环。
  • 在第3步交换前，a 后面的数是按照从大到小进行排列（否则第1步中就可以找到左邻小于右邻的数了）
  • 在交换之后，a 后面的数仍然是按照从大到小排列的，尽管 b 位置的值变成了 list[a]，但是由于 b 位置是第一个比 list[a] 大的，因此交换之后 list[a] 仍然比左邻小，比右邻大。
  • 既然 a 后面的数是从大到小排列的，那么第4步的排序，直接将 a 后面的数倒序即可。

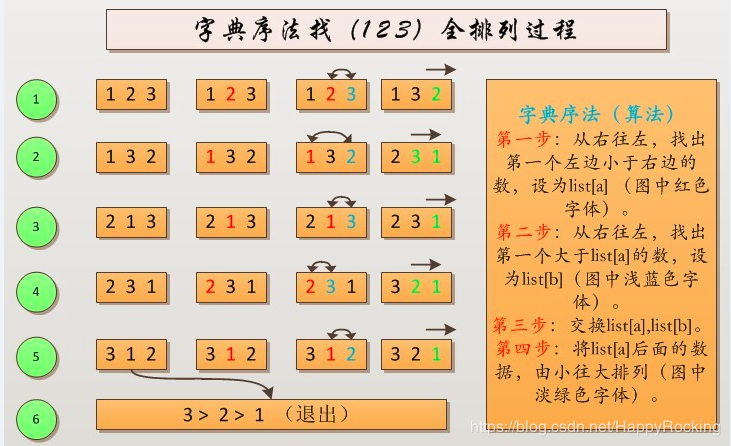
给出1,2,3的一个全排列的示意图：

全排列示意图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

    /**
     * 字典序法
     * 123456789，最后一个是987654321
     * 思想：从右到左若都是增的，也就没有下一个，否则找出第一次出现下降的位置
     * 举例：如何得到346987521的下一个
     * 1. 从尾部往前找第一个P(i-1) < P(i)的位置
     *    3 4 6 <- 9 <- 8 <- 7 <- 5 <- 2 <- 1 ,最终找到6是第一个变小的数字，记录下6的位置i-1
     * 2. 从i位置往后找到最后一个大于6的数
     *    3 4 6 -> 9 -> 8 -> 7 5 2 1， 最终找到7的位置，记录为值为m
     * 3. 交换位置i-1和m的值
     *    3 4 7 9 8 6 5 2 1
     * 4. 倒序i位置后的所有数据
     *    3 4 7 1 2 5 6 8 9, 则347125689为346987521的下一个排列
     * @param str
     * @return java.util.ArrayList<java.lang.String>
     * @author wangming
     * @date 2019/8/26 22:21
     */
    public static ArrayList<String> Permutation2(String str){
        ArrayList<String> list = new ArrayList<>();
        if (str == null || str.length() == 0){
            return list;
        }
        char[] chars = str.toCharArray();
        Arrays.sort(chars);

        list.add(String.valueOf(chars));

        int len = chars.length;
        while (true){
            int lIndex = len - 1;
            int rIndex;
            while (lIndex >= 1 && chars[lIndex - 1]>= chars[lIndex]){
                lIndex--;
            }
            if(lIndex == 0){
                break;
            }
            rIndex = lIndex;
            while (rIndex < len && chars[rIndex] > chars[lIndex - 1]){
                rIndex++;
            }
            swap(chars,lIndex-1,rIndex-1);
            reverse(chars,lIndex);

            list.add(String.valueOf(chars));
        }
        return list;
    }

    private static void reverse(char[] chars, int k){
        if(chars == null || chars.length <= k){
            return;
        }
        int len = chars.length;
        for(int i = 0;i < (len-k)/2;i++){
            //第一个和最后一个开始交换，第二个和倒数第二个开始交换...
            int m = k + i;
            int n = len - 1 - i;
            if(m <= n){
                swap(chars,m,n);
            }
        }
    }

    public static void swap(char[] cha, int i, int j){
        char temp = cha[i];
        cha[i] = cha[j];
        cha[j] = temp;
    }

1.2 字符串的全组合

题目描述

输入一个字符串，输出该字符串中字符的所有组合。举个例子，如果输入abc,它的组合有a,b,c,ab,ac,bc,abc。

1. 递归法

上面我们讨论了如何利用递归的思路来求字符串的全排列，同样，求字符串的全组合也可以采用这种思路。假设我们想在长度为n的字符串中求m个字符的组合。我们先从头扫描字符串的第一个字符。针对第一个字符，我们有两种选择：第一是把这个字符放到组合中去，接下来我们需要在剩下的n-1个字符中选取m-1个字符；第二是不把这个字符放到组合中去，接下来我们需要在剩下的n-1个字符中选择m个字符。这两种选择都很容易用递归实现。给出一个详细的算法思路：

  1. 假设在长度为n的字符串中求m个字符的组合
  2. 从头扫描字符串的第一个字符，有两种选择：
    • (1)把这个字符放到组合中去，接下来我们需要在剩下的n-1个字符中选取m-1个字符
    • (2)不把这个字符放到组合中去，接下来我们需要在剩下的n-1个字符中选择m个字符

Attention:所有字符取出摆放的位置都是以原来的相对位置，不改变原来的前后顺序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

    public static void combination(String str){
        Stack<Character> stack = new Stack<>();
        int len = str.length();
        char[] arrays = str.toCharArray();
        for (int i = 1; i <= len; i++) {
            combine(arrays,0,i,stack);
        }
    }

    //从字符数组中第begin个字符开始挑选number个字符加入到list中
    public static void combine(char[] arrays,int begin, int number, Stack<Character> result){
        if(number == 0){ //边界条件是number取0个，则输出结果
            System.out.println(result.toString());
            return;
        }
        if(begin == arrays.length){
            // 边界条件为错误情况则返回，因为begin已经到最后一个字符之外，根本没有这个索引
            return;
        }
        //stack压入一个元素，表示取此字符，然后begin+1表示在此字符后面取number-1个字符，刚好2-(1)中的情况
        result.push(arrays[begin]);
        combine(arrays,begin+1,number-1,result);
        result.pop();
        //刚才压入栈中的元素弹出，表示不取当前begin位置的字符，从begin+1以后取出number个字符，刚好是2-(2)中的情况
        combine(arrays,begin+1,number,result);
    }

2.位运算实现

基本思路：求组合，表示可以取少于总字符个数的字符组合，因为全字符组合就一个，则假设输入字符个数为n个，则最终输入字符格式为n个，则最终组合结果是(2^n - 1)个。

原因：假设字符为a,b,c，则1表示取c元素，0表示不取c。所以001表示取a，010取b，100取c，011取ab。所以一共三位，每个位上有两个选择0,1.所以是(2^n-1)个结果。依次表示001,010,011,100,101,110,111.对应的输出组合结果为：a,b,ab,c,ac,bc,abc。因此可以循环1~2^n - 1(n为字符串长度)，然后输出对应代表的组合即可。

Attention:这个思路也非常好~ 但是前提是字符长度不超过32个.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

   public static void combination(String str){
        char[] chs = str.toCharArray();
        int len = str.length();
        if(len == 0){
            return;
        }
        int n = 1 << len;
        //从1循环到2^len-1
        for(int i = 0; i < n; i++){ //结果有n个。输出结果是从数字从小到大：即输出0,1,2,3,...,2^n
            for(int j = 0; j < len; j++){ //每个数二进制最多可以左移len次，即遍历完字符在位置上的所有可能
                if((i & (1 << j)) != 0){ //& 表示与。两个位都为1时，结果才为1
                    System.out.print(chs[j]);
                }
            }
            System.out.println();
        }
    }

补充：

  1. j = 0， 1«j 为将第一位置1
  2. j = 1， 1«j 为将第二位置1
  3. j = 2， 1«j 为将第三位置1

参考文章：

July算法习题

含有重复字符的字符串排列组合

2. 最长上升子序列

题目描述

给定一个无序的整数数组，找到其中最长上升子序列的长度。例如，给定数组[10,9,2,5,3,7,101,18],输出的长度为4，因为最长的上升子序列是 [2,3,7,101]，它的长度是 4。

1.暴力法

CATALOG
    FEATURED TAGS
    cluster JAVA 并发编程 Knowledge 二叉树 数据库 Java JavaScript Network Nodejs TCP/IP
    FRIENDS