面经手写算法

“The purpose of human life is to serve, and to show compassion and the will to help others.”

1.手写LRU算法

LRU(Least Recently Used, 最近很少使用)，其具体的设计原则是：如果一个数据在最近一段时间没有被访问到，那么将来它被访问的可能性也很小。也就是说，当限定的空间已存满数据时，应当把最近没有被访问到的数据淘汰。

实现LRU主要有以下几种方法：

用一个数组来存储数据，给每一个数据项标记一个访问时间戳，每次插入新数据项的时候，先把数组中存在的数据项的时间戳自增，并将新数据项的时间戳置为0并插入到数组中。每次访问数组中的数据项的时候，将被访问的数据项的时间戳置为0。当数组空间已满时，将时间戳最大的数据项淘汰。
利用一个链表来实现，每次新插入数据的时候将新数据插到链表的头部；每次缓存命中（即数据被访问），则将数据移到链表头部；那么当链表满的时候，就将链表尾部的数据丢弃。
利用链表和hashmap。当需要插入新的数据项的时候，如果新数据项在链表中存在（一般称为命中），则把该节点移到链表头部，如果不存在，则新建一个节点，放到链表头部，若缓存满了，则把链表最后一个节点删除即可。在访问数据的时候，如果数据项在链表中存在，则把该节点移到链表头部，否则返回-1。这样一来在链表尾部的节点就是最近最久未访问的数据项。

对于第一种方法，需要不停地维护数据项的访问时间戳，另外，在插入数据、删除数据以及访问数据时，时间复杂度都是O(n)。对于第二种方法，链表在定位数据的时候时间复杂度为O(n)。所以在一般使用第三种方式来是实现LRU算法.

1.使用LinkedHashMap实现(快速实现)

LinkedHashMap底层就是HashMap加双链表实现的，而且本身已经实现了按照访问顺序的存储。此外，LinkedHashMap中本身就实现了一个方法removeEldestEntry:用于判断是否需要移除最不常读取的数，方法默认是直接返回false，不会移除元素，所以需要重写该方法。即当缓存满了就移除最不常用的数。

public class LRUCache<K, V> extends LinkedHashMap<K, V>{

    private final int maxCapacity;
    
    private static final float DEFAULT_LOAD_FACTOR = 0.75f;

    private final Lock lock = new ReentrantLock();

    public LRUCache(int maxCapacity){
        super(maxCapacity, DEFAULT_LOAD_FACTOR, true);
        this.maxCapacity = maxCapacity;
    }

    @Override
    protected boolean removeEldestEntry(Map.Entry<K, V> eldest) {
        return size() > maxCapacity;
    }
    @Override
    public boolean containsKey(Object key) {
        try{
            lock.lock();
            return super.containsKey(key);
        }finally {
            lock.unlock();
        }
    }

    @Override
    public V get(Object key) {
        try {
            lock.lock();
            return super.get(key);
        }finally {
            lock.unlock();
        }
    }

    @Override
    public V put(K key, V value) {
        try {
            lock.lock();
            return super.put(key, value);
        }finally {
            lock.unlock();
        }
    }

    @Override
    public int size() {
        try {
            lock.lock();
            return super.size();
        }finally {
            lock.unlock();
        }
    }

    @Override
    public void clear() {
        try {
            lock.lock();
            super.clear();
        }finally {
            lock.unlock();
        }
    }

    public List<Map.Entry<K, V>> getAll(){
        try {
            lock.lock();
            return new ArrayList<Map.Entry<K, V>>(super.entrySet());
        }finally {
            lock.unlock();
        }
    }
}

2.LRUCache的链表加上HashMap的实现

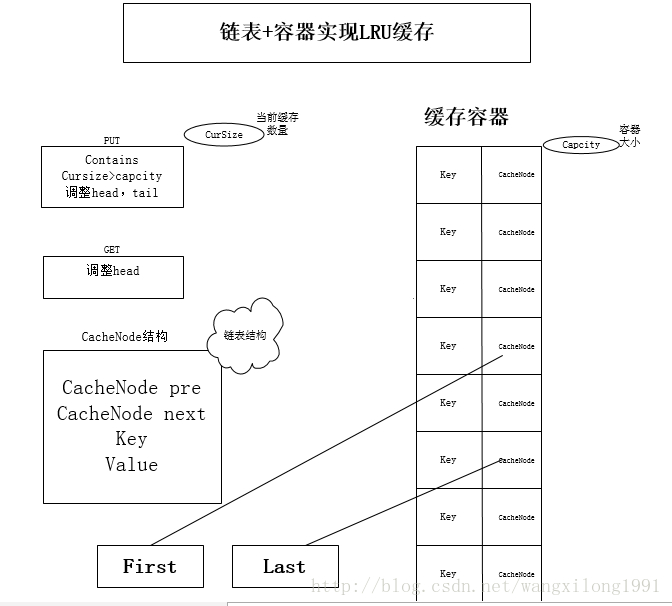
LRU缓存的链表+哈希表实现

将Cache的所有位置都用双链表连接起来，当一个位置被命中之后，就将通过调整链表的指向，将该位置调整到链表头的位置，新加入的Cache直接加到链表头中。这样，在进行多次Cache操作后，最近被命中的，就会被向链表头方向移动，而没有命中的，而想链表后面移动，链表尾则表示最近最少使用的Cache。

public class CacheNode {

    CacheNode pre;
    CacheNode next;
    Object key;
    Object value;
}

public class LRUCache<K, V> {

    private int currentCacheSize;
    private int CacheCapacity;
    private HashMap<K, CacheNode> caches;
    //双向链表的头节点
    private CacheNode first;
    //双向链表的尾节点
    private CacheNode last;

    public LRUCache(int size){
        currentCacheSize = 0;
        this.CacheCapacity = size;
        caches = new HashMap<>(size);
    }

    public void put(K k, V v){
        CacheNode node = caches.get(k);
        if(node == null){
            if(caches.size() >= CacheCapacity){
                caches.remove(last.key);
                removeLast();
            }
            node = new CacheNode();
            node.key = k;
        }
        node.value = v;
        moveToFirst(node);
        caches.put(k,node);
    }

    public Object remove(K k){
        CacheNode node = caches.get(k);
        if(node != null){
            if(node.pre != null){
                node.pre.next = node.next;
            }
            if(node.next != null){
                node.next.pre = node.pre;
            }
            if(node == first){
                first = node.next;
            }
            if(node == last){
                last = node.pre;
            }
        }
        return caches.remove(k);
    }

    public void clear(){
        first = null;
        last = null;
        caches.clear();
    }

    private void moveToFirst(CacheNode node){
        if(first == node){
            return;
        }
        if(node.next != null){
             node.next.pre = node.pre;
        }
        if(node.pre != null){
            node.pre.next = node.next;
        }
        if (node == last){
            last = last.pre;
        }
        if(first == null || last == null){
            first = last = node;
            return;
        }

        node.next = first;
        first.pre = node;
        first = node;
        first.pre = null;
    }

    private void removeLast(){
        if(last != null){
            last = last.pre;
            if(last == null){
                first = null;
            }else{
                last.next = null;
            }
        }
    }

    @Override
    public String toString(){
        StringBuilder sb = new StringBuilder();
        CacheNode node = first;
        while (node != null){
            sb.append(String.format("%s:%s", node.key, node.value));
            node = node.next;
        }
        return sb.toString();
    }
}

2. 求出小于数字N的所有素数

2.1 常规办法求解

开根号法：如果一个数（>2），对这个数求平方根，如果这个数能被这个数的平方根到2之间的任何一个（只要有一个就行）整除说明就不是质数，如果不能就说明是质数！

原理：假如一个数N是合数，它有一个约数a,a×b=N，则a、b两个数中必有一个大于或等于根号N，一个小于或等于根号N。因此，只要小于或等于根号N的数（1除外）不能整除N，则N一定是素数。

    public static List<Integer> getPrimes(int N){
        List<Integer> result = new ArrayList<>();
        for(int i = 1; i <= N; i++){
            if(isPrime(i)){
                result.add(i);
            }
        }
        return result;
    }

    //判断一个数是否是素数
    private static boolean isPrime(int n){
        if( n < 2){
            return false;
        }
        for (int i = 2; i <= Math.sqrt(n); i++){
            //如果被整除
            if(n % i == 0){
                return false;
            }
        }
        return true;
    }

2.2 埃式筛选法(Eratosthenes筛选)

原理：要得到自然是N以内的全部素数，必须把不大于根号N的所有素数的倍数剔除，剩下的就是素数。例如，给出要筛数值的范围n，找出以内的素数。先用2去筛，即把2留下，把2的倍数剔除掉；再用下一个质数，也就是3筛，把3留下，把3的倍数剔除掉；接下去用下一个质数5筛，把5留下，把5的倍数剔除掉；不断重复下去…最终未被删去的数就是素数，这样的时间复杂度是O(nloglogn)。但是这样在效率上有一个问题：一个数会被删去多次，例如42会被2 3 7都删去一遍。

给出埃式筛选法的两个图如下所示：(图1中第二行9忘记删除了)

埃式筛选法

    //方法2：埃式筛选法(Eratosthenes筛选),筛选过程包含N
    public static List<Integer> getPrimes2(int N){
        if(N < 2 ){
           return null;
        }
        if(N > 9999999){
            throw new IllegalArgumentException("输出参数N错误");
        }
        List<Integer> result = new ArrayList<>();
        //假设初始所有数都是素数，且某个数是素数，则其值为0
        long[] array = new long[N+1];
        array[0] = 1; // 0不是素数
        array[1] = 1; // 1不是素数
        //筛选过程
        for (int i = 2; i <= Math.sqrt(N); i++){
            if(array[i] == 0){
                for (long j = i * i; j <= N; j += i){
                    array[j] = 1; //标记该位置为非质数
                }
            }
        }
        //筛选出N以内的所有素数
        for (int i = 0; i < array.length; i++){
            if(array[i] == 0){
                result.add(i);
            }
        }
        return result;
    }

2.3 欧拉筛选

欧拉筛法的基本思想是在埃氏筛法的基础上，让每个合数只被它的最小质因子筛选一次，以达到不重复的目的。

欧拉筛选法的原理

欧拉筛法

对于一个正整数，如果其为合数，那么该数的质因数分解形式是唯一的。现定义：对于某个范围内的任意合数，只能由其最小的质因子将其从表中删除。我们很容易得出该算法的时间复杂度为线性的，为什么呢？因为一个合数的质因数分解式是唯一的，而且我们定义了合数只能由最小质因子将其从表中删除，所以每个合数只进行了一次删除操作(需要注意的是:埃氏素数筛选法中合数可能被多个质数删除，比如12，18等合数).现在原始的问题转换为怎么将合数由其最小的质因子删除？我们考查任何一个数n，假设其最小质因子为m，那么小于等于m的质数与n相乘，会得到一个更大的合数，且其最小质因数为与n相乘的那个质数，而该合数可以直接从表中删除，因为其刚好满足之前的合数删除的定义，所以我们需要维护一个表用来记录已经找到了的质数，然后根据刚才叙述的步骤执行，就能将埃氏素数筛选法的时间复杂度降为O(n)。

    public static int[] getPrimesStatusArray1(int N){
        boolean[] visit = new boolean[N+1];
        Arrays.fill(visit,true);
        int[] prime = new int[N+1];
        int num = 0;
        for (int i = 2; i <= N;i++){
            if(visit[i]){
                prime[num++] = i;
            }
            //此处边界判断为rec[j] <= n / i,如果写成i * rec[j] <= n,需要确保i * rec[j]不会溢出int
            for(int j = 0; j < num && prime[j] <= N / i; ++j){
                visit[i*prime[j]] = false;
                if(i % prime[j] == 0){
                    break;
                }
            }
        }
        return prime;
    }

"手写算法总结"